Dropout Regularization Implemented

We will gain a deeper understanding of dropout behavior during inference time and implement from scratch

Introduction

Dropout regularization is a simple and yet powerful technique used in neural networks to prevent overfitting. It was first introduced in the research paper “Dropout: A Simple Way to Prevent Neural Networks from Overfitting”.

In this post, we will understand dropout by implementing from scratch and integrating it with mininn library.

Description

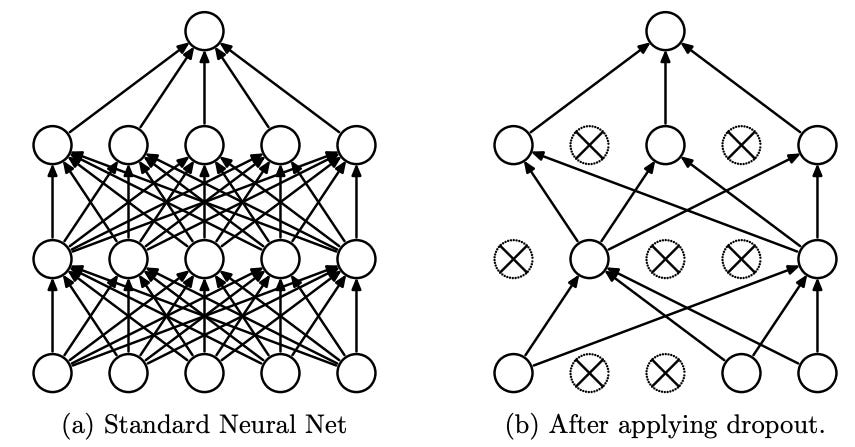
Dropout works by randomly deactivating units in a neural network during training. These deactivated units are temporarily excluded from both the forward and backward passes, including their incoming and outgoing connections, as shown in the picture below:

Figure 1 from the original paper

During each mini-batch training step, dropout randomly samples a new thinned neural network by dropping each unit with a fixed probability p, independently of other units. This process effectively treats a network with n units as a collection of 2^n smaller subnetworks. By training with dropout, we're essentially training an ensemble of 2^n subnetworks with extensive weight sharing. Fundamentally, this ensemble approach is key to reducing the model’s variance, which in turn minimizes overfitting and improves its ability to generalize to new, unseen data.

During Training

Lets say we’re training a single layer feedforward neural network:

\(\begin{align} nn(X)=f(XW+b) \end{align}\)

where:

• X is batched input of shape (batch size, n)

• W is a weight matrix of shape (n, n)

• b is a bias vector of shape (n,)

• f is a non-linear activation function, e.g., relu or sigmod

With dropout, our single layer feedforward neural network becomes:

\(nn(X)=f((X \odot M)W+b )\)

• M is a mask of shape (batch size, n) sampled from a Bernoulli distribution, where each element is sampled identically and independently of each other

• ⊙ is element-wise multiplication

We simply need to add more parameters to a feedforward neural network with two or more layers using dropout:

\(\begin{align} nn(X)=f(f((X \odot M_1)W_1+b_1)\odot M_2)W_2+b_2) \end{align}\)

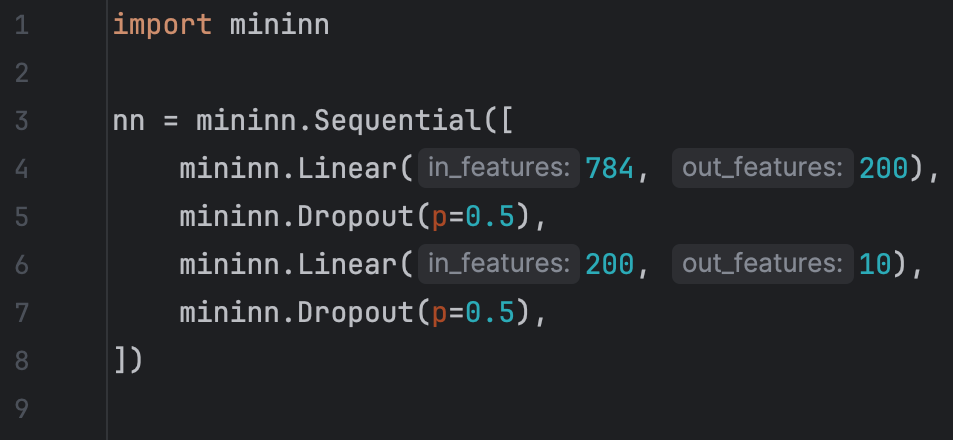
We can implement the Dropout layer in a modular way within the mininn library, allowing us to define our two or more layer feedforward neural network as follows:

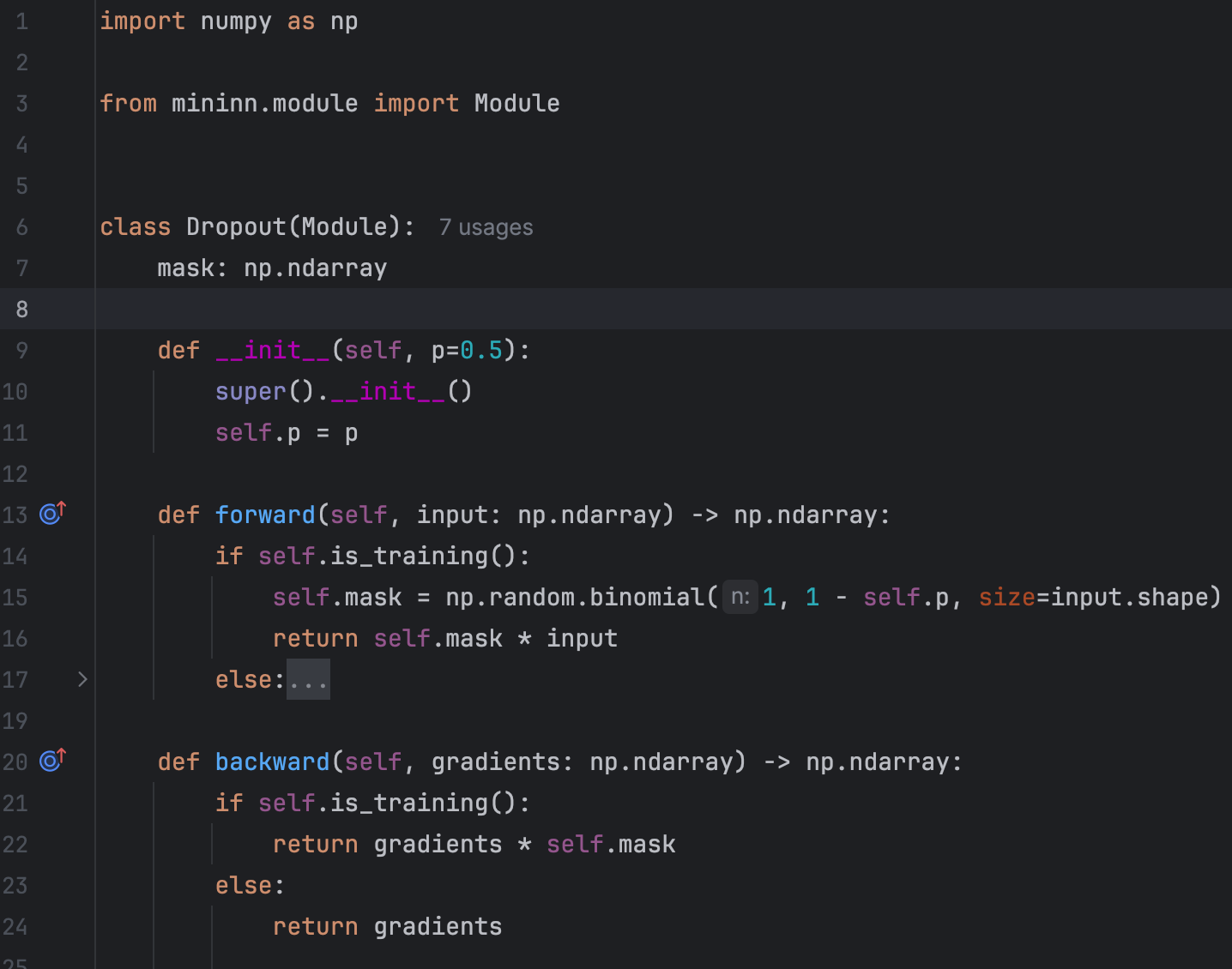
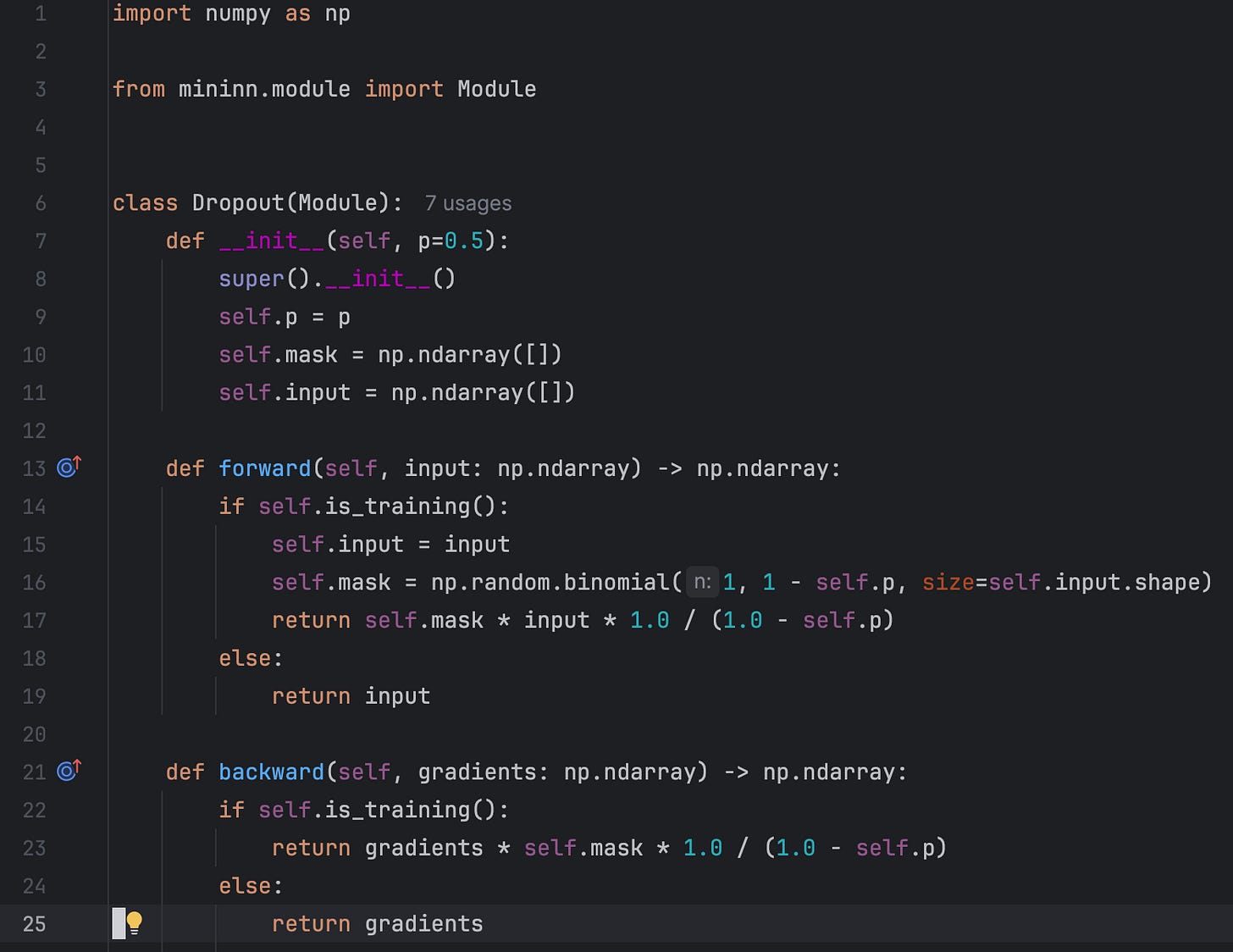
Essentially, Dropout receives an input tensor and randomly sets some elements of the input tensor to zero:

We used numy.random.binomial to generate a mask of the same shape as the input: 0 with probability p or 1 with probability 1-p. Very simple!

During Inference

Ideally, we should ensemble all 2^n subnetworks at inference by averaging their outputs. However, since sampling 2^n subnetworks is impractical, we need to either calculate the expected average analytically or find a close approximation.

We can exactly calculate the expected output as long as we use an activation function with the following property:

\(\begin{align} \mathbb{E}[f(X)]=f(\mathbb{E}[X]) \end{align}\)

This property holds for any linear or piecewise linear activations such as ReLU.

Assuming that the above property holds:

\(\begin{align} \mathbb{E}_M[nn(X)]&= \mathbb{E}_M[f((X \odot M)W+b)]\\ &= f(\mathbb{E}_M[(X \odot M)W+b])\\ &= f((X \odot \mathbb{E}_M[M])W+b)\\ \end{align}\)

Since M is sampled from a Bernoulli distribution, it is expected value is E[M]=1-p. Hence:

\(\begin{align} \mathbb{E}_M[nn(X)]=f(X(1-p)W+b) \end{align}\)

We can derive a similar expected value for two layer feedforward network:

\(\begin{align} \mathbb{E}_M[nn(X)]=f(f(X(1-p)W_1+b_1)(1-p)W_2 + b_2) \end{align}\)

Nice! It nearly looks like a forward pass without dropout; we simply need to adjust the inputs of the Dropout layers by scaling them by (1-p) during inference. This allows us to perform a forward pass a single time instead of multiple times (up to 2^n).

The above property isn’t exact for sigmoid activation; however, it still provides a close approximation. In fact, it results in the expected value of the normalized weighted geometric mean as defined in “Understanding Dropout“.

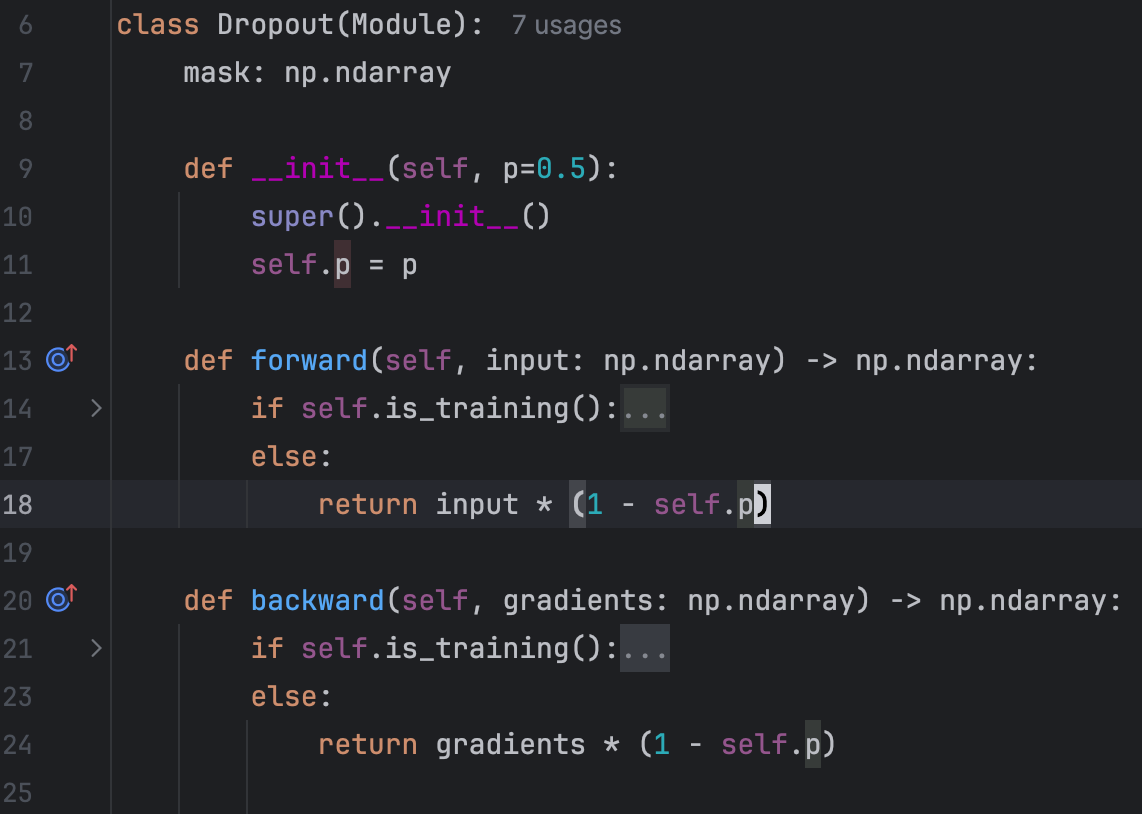
The implementation during inference is also very simple. See the “else” branch:

Implementation

The final implementation differs slightly from what we've previously discussed. Specifically:

• During inference, we pass the input without any modifications

• During training, we scale the output by 1/(1-p) to match the expected value during inference.

This behavior is exactly the same as PyTorch Dropout. You can see the full implementation dropout.py in mininn library.

The End

Hope you enjoyed the post.